Find the Solutions to 3x-y7 11mod13
Part 6 : Gaussian Elimination
![]()
Gaussian elimination is an algorithm for solving system of linear equations. It is named after Carl Friedrich Gauss , a German mathematician.

It is similar to elimination method discussed earlier.
To perform Gaussian Elimination :
- We create augmented matrix of coefficients and constants of given system of linear equations.
- We select our pivot (which is the first element in diagonal). Then we try to reduce all elements below it (to "0"), using pivot.
We do this by performing two kind of operations :
a) Multiplying pivot row (row of pivot element) with a scalar quantity and subtracting or adding it rows below it.
b) Interchanging rows (like row 2 is exchanged with row 3)
Then, we select next pivot (next element in diagonal) and reduce elements below it.
3. We brea k augmented matrix back into row picture and perform multiplication with variable matrix. We get new reduced equations.
We solve those equations to get values of unknowns (variables).
Performing Gaussian Elimination
Assuming, that we have to find solution(s) to following system of equations :
4x+y = 9→(1)
2x-y = 3→(2)
5x-3y = 7→(3)
("One unique solution" example from Part 5)
Step 1 (Making augmented matrix) :
To perform Gaussian elimination we take the row picture of (1), (2) and (3). Which would be as follows:
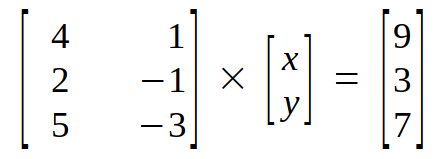
Next, we make an augmented matrix for coefficient matrix and constant matrix.
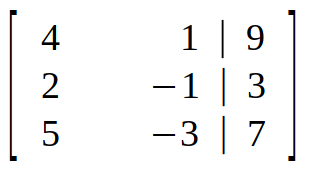
Step 2 (Elimination) :
Step 2A:
Taking element in top left corner (first element in diagonal) as pivot, we aim to eliminate (reduce to "0") all the elements below it. In other words, we have to convert every element in column 1 to "0" except pivot.
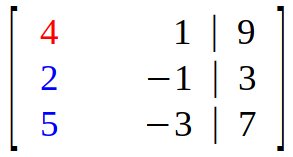
So, we multiply first row with scalar 1/2 and subtract it from second row.
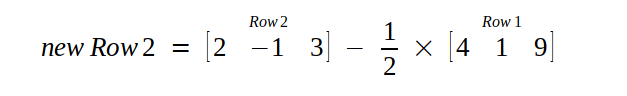
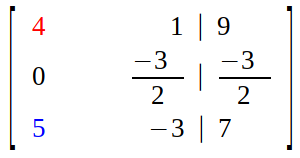
Then, we multiply first row with scalar 5/4 and subtract from third row.
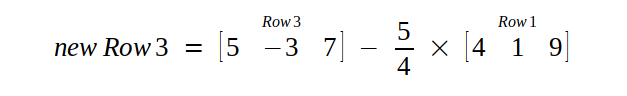
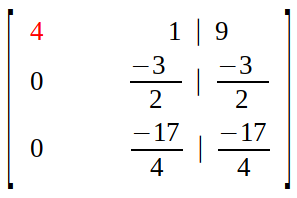
Now all the elements in first column are "0" except pivot.
Step 2B :
Now next element in diagonal (second column second row) is set as pivot, and we aim to eliminate all the elements below it.
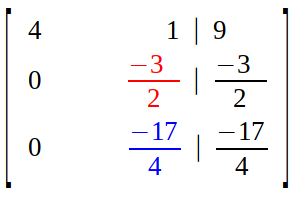
So, we multiply second row with scalar 17/6 and subtract it from third row.

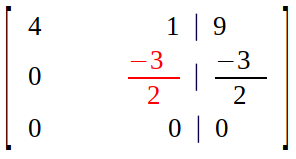
Result is an upper triangular matrix.
The current state of augmented matrix is called row echelon form.
Step 3 (Back Substitution) :
Now, we convert row echelon form back into row picture.
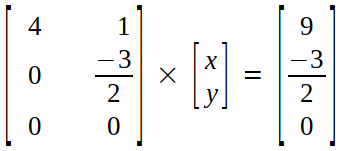
On multiplying, we get :
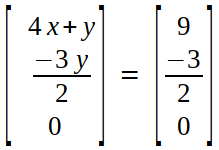
4x + y = 9 →(4)
-3y/2 = -3/2 →(5)
Solving (5) for "y", we get :
y =1
Now, we substitute y=1 in (4) :
4x + 1 = 9
4x = 8
x = 2
So, we get x=2 and y=1, exactly what we got when we solved through row picture and column picture in Part 5.
Now, we apply same algorithm in two more cases (infinitely many solutions and no solution).
Infinitely Many Solutions
We take the same example as in Part 5. That is :
x+2y = 4→(6)
2x+4y = 8→(7)
Step 1 (Making augmented matrix) :
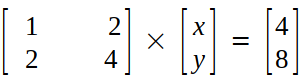
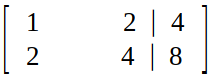
Step 2 (Elimination) :
Taking first element is diagonal ("1") as pivot.
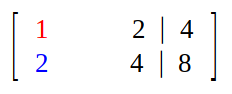
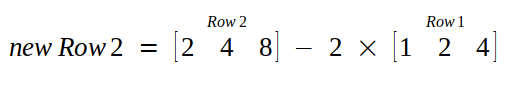

We do not any more pivots as there is nothing to eliminate.
Step 3 (Back Substitution) :
We convert row echelon form back into row picture :
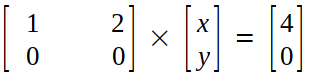
x + 2y = 4 →(8)
Equation (6) and equation (8) are same, and we have only one equation after elimination but two unknowns ("x" and "y").
There are a lot of values that could be substituted for x and y to satisfy (8).
Like, x=0 and y=2. Substituting in equation (8) we get :
0 + 2(2) = 4
4 = 4
Or x=1 and y=1.5 . Substituting in equation (8) we get :
1 + 2(1.5) = 4
1 + 3 = 4
4 = 4
Thus, system of equations (6) and (7) has infinitely many solutions.
No Solution
Considering a system of linear equations as follows :
x+y = 4→(9)
x+y = 8→(10)
x-y = 0→(11)
Applying Gaussian Elimination.
Step 1 (Making Augmented Matrix) :
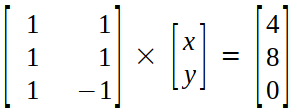
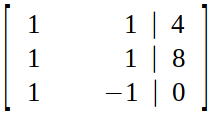
Step 2 (Elimination) :
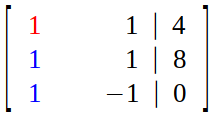
We perform following two operations :
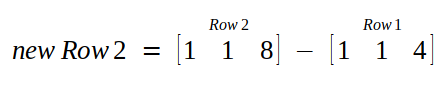

and the matrix we get is :
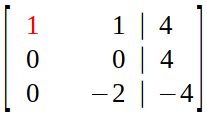
We still don't have a row echelon form (upper triangular matrix).
So, we do row exchange (which is also an option in elimination step of Gaussian Elimination) :
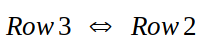
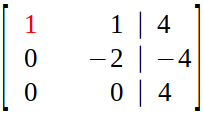
Step 3 (Back Substitution) :
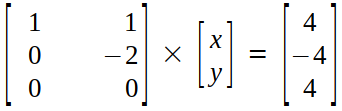
The equations we get after multiplying the matrices above :
x + y = 4 → (12)
-2y = -4 → (13)
Solving equation (13) for "y", we get:
y = 2
Substituting y=2 in equation (12), we get:
x + 2 = 4
x = 2
To confirm x = 2 and y =2 is the solution, we substitute them in system of equations i.e. (9), (10) and (11).
Substituting in (9), we get :
2 + 2 = 4
4 = 4
x=2 and y=2, satisfies (9).
Substituting in (10), we get :
2 + 2 = 8
4 ≠ 8, it does not satisfy (10).
Therefore, x=2 and y=2 is not a solution to (9), (10) and (11) and there exists no solution to this system of linear equations as we saw in last article.
When do we encounter one of three cases (one solution, infinitely many solutions and no solution) ?
One Solution
When number of unknowns (variables) is equal to the number of equation in system of linear equations .
Taking example of (1), (2) and (3) :
4x+y = 9→(1)
2x-y = 3→(2)
5x-3y = 7→(3)
There are 2 unknowns ("x" and "y") and 3 equations ((1),(2) and (3)).
Two equations would've been enough for 2 unknowns.
Infinitely Many Solutions
When number of unknowns exceeds the number of equations.
Taking example of (6) and (7) :
x+2y = 4→(6)
2x+4y = 8→(7)
There are 2 unknowns ("x" and "y") and 2 equations ((6) and (7)).
But if we look further, we will notice that (7) is just (6) multiplied with 2. Hence, (6) and (7) are same equations. Thus, number of equations is 1.
No Solution
Generally, when number of equations exceed the number of unknowns. It has no solution.
But, it is also necessary that no value could be substituted for unknowns such the system of linear equation is satisfied. For that, we should check twice if solution obtained satisfies all the equations in system.
Find the Solutions to 3x-y7 11mod13
Source: https://medium.com/linear-algebra/part-6-gaussian-elimination-b1ad4a279a74