Find Number of Solutions With Multiple Variables

Linear Equations in Two Variables

Linear equations in two variables are a system of equations with a unique solution, no solutions, or infinitely many solutions. A linear system of equations may have 'n' number of variables. An important thing to keep in mind while solving linear equations with n number of variables is that there must be n equations to solve and determine the value of variables. The set of solutions obtained on solving these linear equations is a straight line. Linear equations in two variables are the algebraic equations which are of the form y = mx + b, where m is the slope and b is the y-intercept. They are the equations of the first order. For example, y = 2x+3 and 2y = 4x + 9 are two-variable linear equations.

1.	What are Linear Equations in Two Variables?
2.	Forms of Linear Equations in Two Variables
3.	Methods of Solving Linear Equations in Two Variables
4.	FAQs

What are Linear Equations in Two Variables?

The linear equations in two variables are of the highest exponent order of 1 and have one, none, or infinitely many solutions. The standard form of a two-variable linear equation is ax+ by+ c= 0 where x and y are the two variables. The solutions can also be written in ordered pairs. The graphical representation of the linear equations in two variables includes two straight lines which could be intersecting lines, parallel lines, or coincident lines.

Forms of Linear Equations in Two Variables

A linear equation in two variables can be in different forms like standard form, intercept form and point-slope form. For example, the same equation 2x+3y=9 can be represented in each of the forms like 2x+3y-9=0 (standard form), y = (-2/3)x + 3 (slope-intercept form), and y - 5/3 = -2/3(x + (-2)) (point-slope form). Look at the image given below showing all these three forms of representing linear equations in two variables with examples.

The system of equations means the collection of equations. We will learn how to solve linear equations in two variables using different methods.

Methods of Solving Linear Equations in Two Variables

There are five methods to solve a system of linear equations in two variables. Those methods are explained below:

• Graphical Method
• Substitution Method
• Cross Multiplication Method
• Elimination Method
• Determinant Method

Graphical Method for Solving Linear Equations in Two Variables

The steps to solve linear equations in two variables graphically are given below:

• Step 1: To solve a system of two equations in two variables graphically, we graph each equation.
• Step 2: To graph an equation manually, first convert it to the form y=mx+b by solving the equation for y.
• Step 3: Start putting the values of x as 0, 1, 2, and so on and find the corresponding values of y, or vice-versa.
• Step 4: Identify the point where both lines meet.
• Step 5: The point of intersection is the solution of the given system.

Example: Find the solution of the following system of equations graphically.
-x+2y-3 =0
3x+4y-11=0
Solution: We will graph them and see whether they intersect at a point. As you can see below, both lines meet at (1, 2). Thus, the solution of the given system of linear equations is x=1 and y=2.

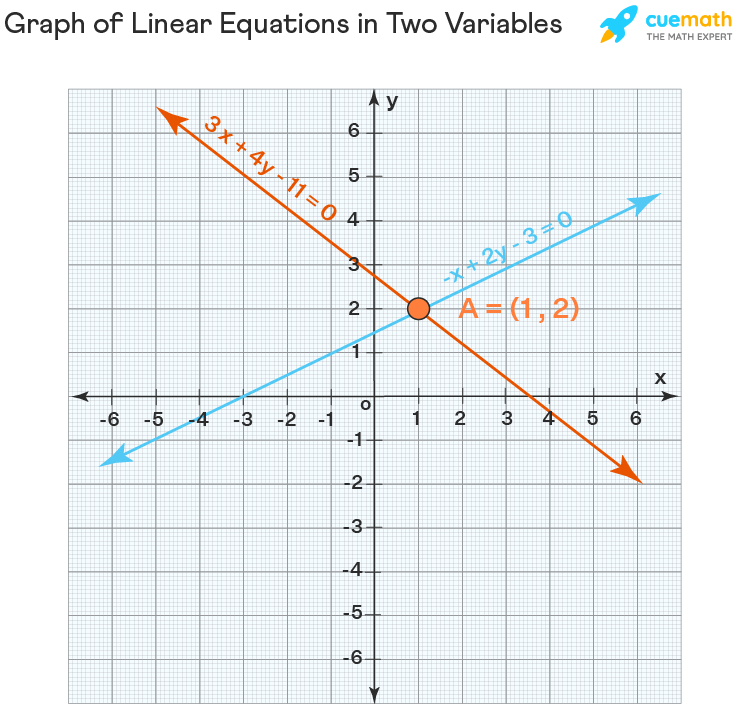
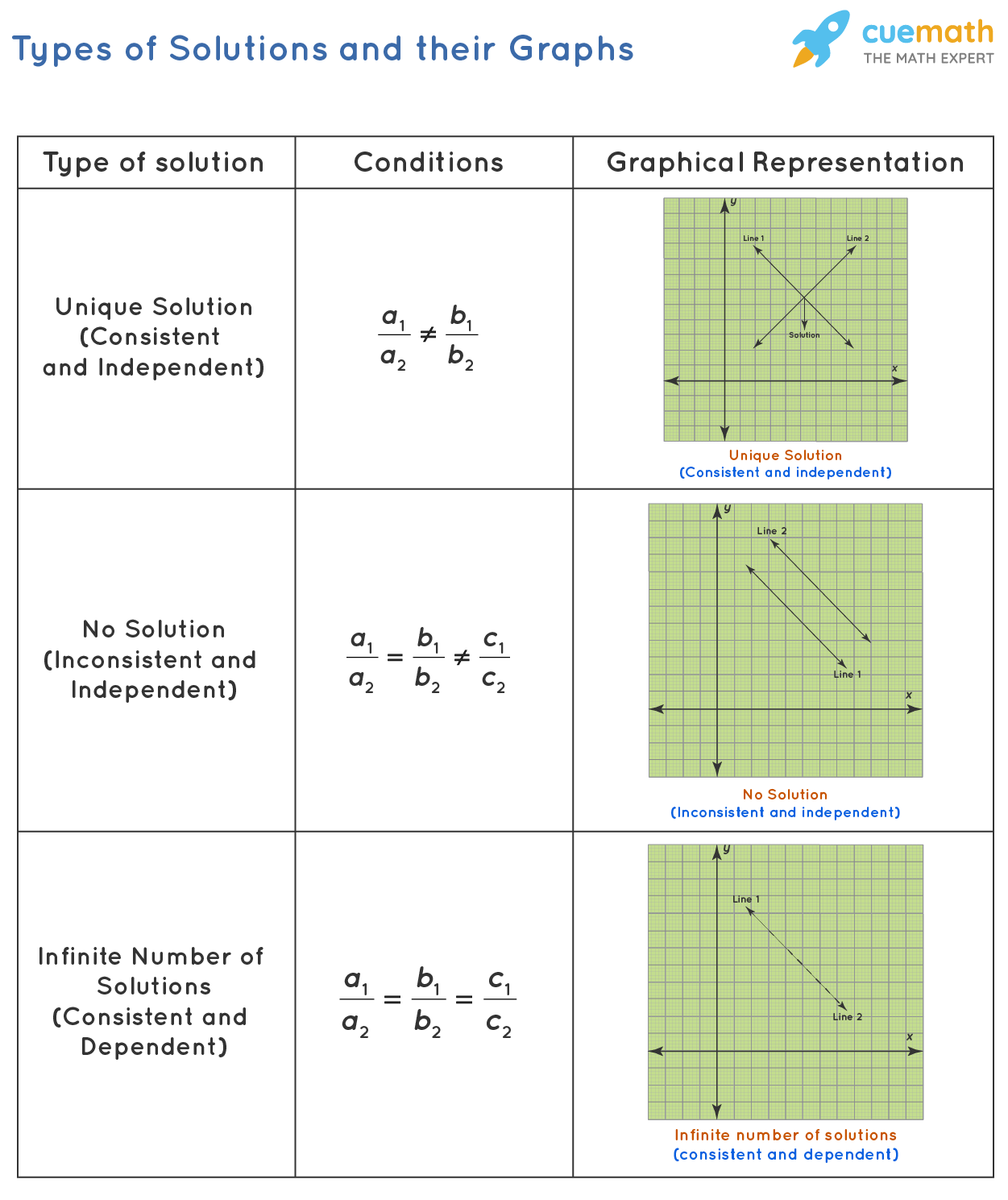
But both lines may not intersect always. Sometimes they may be parallel. In that case, the system of linear equations in two variables has no solution. In some other cases, both lines coincide with each other. In that case, each point on that line is a solution of the given system and hence the given system has an infinite number of solutions. If the system has a solution, then it is said to be consistent; otherwise, it is said to be inconsistent.

Consider a system of two linear equations: \(a_{1}\)x + \(b_{1}\)y + \(c_{1}\) = 0 and \(a_{2}\)x + \(b_{2}\)y + \(c_{2}\) = 0.

Method of Substitution

To solve a system of two linear equations in two variables using the substitution method, we have to use the steps given below:

• Step 1: Solve one of the equations for one variable.
• Step 2: Substitute this in the other equation to get an equation in terms of a single variable.
• Step 3: Solve it for the variable.
• Step 4: Substitute it in any of the equations to get the value of another variable.

Example: Solve the following system of equations using the substitution method.
x+2y-7=0
2x-5y+13=0

Solution: Let us solve the equation, x+2y-7=0 for y:
x+2y-7=0
⇒2y=7-x
⇒ y=(7-x)/2

Substitute this in the equation, 2x-5y+13=0:

2x-5y+13=0
⇒ 2x-5((7-x)/2)+13=0
⇒ 2x-(35/2)+(5x/2)+13=0
⇒ 2x + (5x/2) = 35/2 - 13
⇒ 9x/2 = 9/2
⇒ x=1

Substitute x=1 this in the equation y=(7-x)/2:
y=(7-1)/2 = 3
Therefore, the solution of the given system is x=1 and y=3.

Cross Multiplication Method

Consider a system of linear equations: \(a_{1}\)x + \(b_{1}\)y + \(c_{1}\) = 0 and \(a_{2}\)x + \(b_{2}\)y + \(c_{2}\) = 0.

To solve this using the cross multiplication method, we first write the coefficients of each of x and y and constants as follows:

Here, the arrows indicate that those coefficients have to be multiplied. Now we write the following equation by cross multiplying and subtracting the products.
\(\dfrac{x}{b_{1} c_{2}-b_{2} c_{1}}=\dfrac{y}{c_{1} a_{2}-c_{2} a_{1}}=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}}\)

From this equation, we get two equations:

\(\begin{align}
\dfrac{x}{b_{1} c_{2}-b_{2} c_{1}}&=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}} \\[0.2cm] \dfrac{y}{c_{1} a_{2}-c_{2} a_{1}}&=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}}
\end{align}\)

Solving each of these for x and y, the solution of the given system is:

\(\begin{align}
x&=\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\\[0.2cm] y&=\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}
\end{align}\)

Method of Elimination

To solve a system of linear equations in two variables using the elimination method, we will use the steps given below:

• Step 1: Arrange the equations in the standard form: ax+by+c=0 or ax+by=c.
• Step 2: Check if adding or subtracting the equations would result in the cancellation of a variable.
• Step 3: If not, multiply one or both equations by either the coefficient of x or y such that their addition or subtraction would result in the cancellation of any one of the variables.
• Step 4: Solve the resulting single variable equation.
• Step 5: Substitute it in any of the equations to get the value of another variable.

Example: Solve the following system of equations using the elimination method.
2x+3y-11=0
3x+2y-9=0

Adding or subtracting these two equations would not result in the cancellation of any variable. Let us aim at the cancellation of x. The coefficients of x in both equations are 2 and 3. Their LCM is 6. We will make the coefficients of x in both equations 6 and -6 such that the x terms get canceled when we add the equations.

3 × (2x+3y-11=0)
⇒ 6x+9y-33=0
-2 × (3x+2y-9=0)
⇒ -6x-4y+18=0

Now we will add these two equations:
6x+9y-33=0
-6x-4y+18=0
On adding both the above equations we get,
⇒ 5y-15=0
⇒ 5y=15
⇒ y=3

Substitute this in one of the given two equations and solve the resultant variable for x.
2x+3y-11=0
⇒ 2x+3(3)-11=0
⇒ 2x+9-11=0
⇒ 2x=2
⇒ x=1

Therefore, the solution of the given system of equations is x=1 and y=3.

Determinant Method

The determinant of a 2 × 2 matrix is obtained by cross multiplying elements starting from the top left corner and subtracting the products.

Consider a system of linear equations in two variables: \(a_{1}\)x + \(b_{1}\)y = \(c_{1}\) and \(a_{2}\)x + \(b_{2}\)y = \(c_{2}\). To solve them using the determinants method (which is also known as Crammer's Rule), follow the steps given below:

• We first find the determinant formed by the coefficients of x and y and label it Δ.
  Δ = \[\left|\begin{array}{ll}a_1 & b_1 \\a_2 & b_2\end{array}\right| = a_1 b_2 - a_2b_1\]
• Then we find the determinant \(\Delta_x\) which is obtained by replacing the first column of Δ with constants.
  \(Δ_{x}\) = \[\left|\begin{array}{ll}c_1 & b_1 \\c_2 & b_2\end{array}\right| = c_1 b_2 - c_2b_1\]
• We then find the determinant \(\Delta_y\) which is obtained by replacing the second column of Δ with constants.
  \(Δ_{y}\) = \[\left|\begin{array}{ll}a_1 & c_1 \\a_2 & c_2\end{array}\right| = a_1 c_2 - a_2c_1\]

Now, the solution of the given system of linear equations is obtained by the formulas:

x = \(Δ_{x}\)/Δ
y = \(Δ_{y}\)/Δ

Tips to Remember

While solving the equations using either the substitution method or the elimination method:

• If we get an equation that is true (i.e., something like 0 = 0, -1 = -1, etc), then it means that the system has an infinite number of solutions.
• If we get an equation that is false (i.e., something like 0 = 2, 3 = -1, etc), then it means that the system has no solution.

Topics Related to Linear Equations in Two Variables

Check these articles related to the concept of linear equations in two variables in maths.

• Equation
• Solutions of a Linear Equation
• Simultaneous Linear Equations
• Solving Linear Equations Calculator
• Equation Calculator
• System of Equations Calculator
• Linear Graph Calculator
• Linear Equation Formula
• Linear Equations in One Variable
• Applications of Linear Equations

Linear Equations in Two Variables Examples

1. Example 1: The sum of the digits of a two-digit number is 8. When the digits are reversed, the number is increased by 18. Find the number.
   Solution: Let us assume that x and y are the tens digit and the ones digit of the required number. Then the number is 10x+y.
   And the number when the digits are reversed is 10y+x.
   The question says, "The sum of the digits of a two-digit number is 8".
   So from this, we get a linear equation in two variables: x+y=8.
   ⇒ y=8-x
   Also, when the digits are reversed, the number is increased by 18.
   So, the equation is 10y+x =10x+y+18
   ⇒ 10(8-x)+x =10x+(8-x)+18 (by substituting the value of y)
   ⇒ 80-10x+x =10x+8-x+18
   ⇒ 80-9x=9x+26
   ⇒ 18x = 54
   ⇒ x=3

   Substituting x=3 in y=8-x, we get,
   ⇒ y = 8-3 = 5
   ⇒ 10x+y=10(3)+5 =35
   ⇒ The required number is 35.

2. Example 2: Jake's piggy bank has 11 coins (only quarters or dimes) that have a total value of $1.85. How many dimes and quarters does the piggy bank has?
   Solution: Let us assume that the number of dimes be x and the number of quarters be y in the piggy bank. Let us form linear equations in two variables based on the given information.

   Since there are 11 coins in total, x+y=11 ⇒ y=11-x.
   We know that, 1 dime = 10 cents and 1 quarter = 25 cents.
   The total value of the money in the piggy bank is $1.85 (185 cents).

   Thus we get the equation 10x + 25y = 185
   ⇒ 10x + 25(11-x) = 185 (as y = 11-x)
   ⇒ 10x + 275 - 25x =185
   ⇒ -15x +275 =185
   ⇒ -15x=-90
   ⇒ x = 6

   Substitute this value of x in x+y=11.
   ⇒ y=11-6=5
   Therefore, the number of dimes is 6 and the number of quarters is 5.

3. Example 3: In a river, a boat can travel 30 miles upstream in 2 hours. The same boat can travel 51 miles downstream in 3 hours. Find,

   • What is the speed of the boat in still water?
   • What is the speed of the current?

   Solution: Let us assume that:

   • the speed of the boat in still water = x miles per hour
   • the speed of current = y miles per hour.

   During upstream, the current pulls back the boat's speed and the speed of the boat during upstream = (x-y). During downstream, the current's speed adds to the boat's speed and the speed of the boat during downstream = (x+y).

   Thus,

   	Distance (d)	Time (t)	Speed	Speed = (d/t)
   Upstream	30	2	(x-y)	30/2=15
   Downstream	51	3	(x+y)	51/3=17

   Using the last two columns of the table, we can form linear equations in two variables:
   x-y=15
   x+y=17

   Adding both the equations we get:
   2x = 32
   ⇒ x=16

   Substitute x=16 in x+y=17
   16+y= 17
   y=1

   Therefore, the speed of the boat is 16 miles per hour and the speed of the current is 1 mile per hour.

go to slidego to slidego to slide

Great learning in high school using simple cues

Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.

Book a Free Trial Class

Practice Questions on Linear Equations in Two Variables

go to slidego to slide

FAQs on Linear Equations in Two Variables

What are Linear Equations in Two Variables?

A linear equation is an equation with degree 1. A linear equation in two variables is a type of linear equation in which there are 2 variables present. For example, 2x - y = 45, x+y =35, a-b = 45 etc.

How do you Identify Linear Equations in Two Variables?

We can identify a linear equation in two variables if it is expressed in the form ax+by+ c = 0, consisting of two variables x and y and the highest degree of the given equation is 1.

Can You Solve a Linear Equation in Two Variables?

Yes, we can solve an equation in two variables using different methods and ensuring there are two equations present in the given system of equations so as to obtain the values of variables. If there is one solution it means that the given lines are intersecting, if there is no solution possible, then it means that the given equations are of parallel lines. If there are infinitely many solutions possible, it means that the given equations are forming coincident lines.

How to Graphically Represent Linear Equations in Two Variables?

We can represent linear equations in two variables graphically using the steps given below:

• Step 1: A system of two equations in two variables can be solved graphically by graphing each equation by converting it to the form y=mx+b by solving the equation for y.
• Step 2: The points where both lines meet are identified.
• Step 3: The point of intersection is the solution of the given system of linear equations in two variables.

How Does One Solve the System of Linear Equations in Two Variables?

We have different methods to solve the system of linear equations:

• Graphical Method
• Substitution Method
• Cross Multiplication Method
• Elimination Method
• Determinant or Matrix Method

How Many Solutions Does a Linear Equation with Two Variables Have?

Suppose we have \(a_{1}\)x + \(b_{1}\)y + \(c_{1}\) = 0 and \(a_{2}\)x + \(b_{2}\)y + \(c_{2}\) = 0. The solutions of a linear equation with two variables are:

• One and unique if \(a_{1}\)/\(a_{2}\) ≠ \(b_{1}\)/\(b_{2}\)
• None if \(a_{1}\)/\(a_{2}\) = \(b_{1}\)/\(b_{2}\) ≠ \(c_{1}\)/\(c_{2}\)
• Infinitely many if \(a_{1}\)/\(a_{2}\) = \(b_{1}\)/\(b_{2}\) = \(c_{1}\)/\(c_{2}\)

How is a Linear Inequality in Two Variables like a Linear Equation in Two Variables?

A linear inequality in two variables and a linear equation in two variables have the following things in common:

• The degree of a linear equation and linear inequality is always 1.
• Both of them can be solved graphically.
• The way to solve a linear inequality is the same as linear equations except that it is separated by an inequality symbol.

Find Number of Solutions With Multiple Variables

Source: https://www.cuemath.com/algebra/linear-equations-in-two-variables/

Share :