Find a General Solution to the Cauchy-euler Equation

Ordinary differential equation

In mathematics, an Euler–Cauchy equation, or Cauchy–Euler equation, or simply Euler's equation is a linear homogeneous ordinary differential equation with variable coefficients. It is sometimes referred to as an equidimensional equation. Because of its particularly simple equidimensional structure the differential equation can be solved explicitly.

The equation [edit]

Let y ⁽ⁿ⁾ (x) be the nth derivative of the unknown function y(x). Then a Cauchy–Euler equation of order n has the form

$${\displaystyle a_{n}x^{n}y^{(n)}(x)+a_{n-1}x^{n-1}y^{(n-1)}(x)+\dots +a_{0}y(x)=0.}$$

The substitution ${\displaystyle x=e^{u}}$ (that is, ${\displaystyle u=\ln(x)}$ ; for ${\displaystyle x<0}$ , one might replace all instances of ${\displaystyle x}$ by ${\displaystyle |x|}$ , which extends the solution's domain to ${\displaystyle R_{0}}$ ) may be used to reduce this equation to a linear differential equation with constant coefficients. Alternatively, the trial solution ${\displaystyle y=x^{m}}$ may be used to directly solve for the basic solutions.^[1]

Second order – solving through trial solution [edit]

Typical solution curves for a second-order Euler–Cauchy equation for the case of two real roots

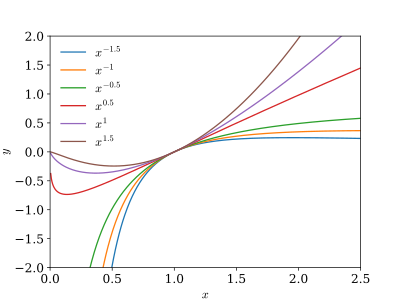
Typical solution curves for a second-order Euler–Cauchy equation for the case of a double root

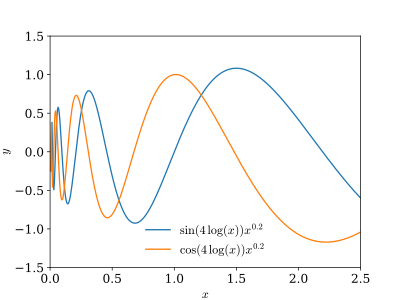
Typical solution curves for a second-order Euler–Cauchy equation for the case of complex roots

The most common Cauchy–Euler equation is the second-order equation, appearing in a number of physics and engineering applications, such as when solving Laplace's equation in polar coordinates. The second order Cauchy–Euler equation is^{[1] [2]}

$${\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+ax{\frac {dy}{dx}}+by=0.}$$

We assume a trial solution^[1]

$${\displaystyle y=x^{m}.}$$

Differentiating gives

$${\displaystyle {\frac {dy}{dx}}=mx^{m-1}}$$

and

$${\displaystyle {\frac {d^{2}y}{dx^{2}}}=m\left(m-1\right)x^{m-2}.}$$

Substituting into the original equation leads to requiring

$${\displaystyle x^{2}\left(m\left(m-1\right)x^{m-2}\right)+ax\left(mx^{m-1}\right)+b\left(x^{m}\right)=0}$$

Rearranging and factoring gives the indicial equation

$${\displaystyle m^{2}+\left(a-1\right)m+b=0.}$$

We then solve for m. There are three particular cases of interest:

• Case 1 of two distinct roots, m ₁ and m ₂ ;
• Case 2 of one real repeated root, m;
• Case 3 of complex roots, α ± βi .

In case 1, the solution is

$${\displaystyle y=c_{1}x^{m_{1}}+c_{2}x^{m_{2}}}$$

In case 2, the solution is

$${\displaystyle y=c_{1}x^{m}\ln(x)+c_{2}x^{m}}$$

To get to this solution, the method of reduction of order must be applied after having found one solution y = x ^m .

In case 3, the solution is

$${\displaystyle y=c_{1}x^{\alpha }\cos(\beta \ln(x))+c_{2}x^{\alpha }\sin(\beta \ln(x))}$$

$${\displaystyle \alpha =\operatorname {Re} (m)}$$

$${\displaystyle \beta =\operatorname {Im} (m)}$$

For ${\displaystyle c_{1},c_{2}\in \mathbb {R} }$ .

This form of the solution is derived by setting x = e ^t and using Euler's formula

Second order – solution through change of variables [edit]

$${\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+ax{\frac {dy}{dx}}+by=0}$$

We operate the variable substitution defined by

$${\displaystyle t=\ln(x).}$$

$${\displaystyle y(x)=\varphi (\ln(x))=\varphi (t).}$$

Differentiating gives

$${\displaystyle {\frac {dy}{dx}}={\frac {1}{x}}{\frac {d\varphi }{dt}}}$$

$${\displaystyle {\frac {d^{2}y}{dx^{2}}}={\frac {1}{x^{2}}}\left({\frac {d^{2}\varphi }{dt^{2}}}-{\frac {d\varphi }{dt}}\right).}$$

Substituting ${\displaystyle \varphi (t)}$ the differential equation becomes

$${\displaystyle {\frac {d^{2}\varphi }{dt^{2}}}+(a-1){\frac {d\varphi }{dt}}+b\varphi =0.}$$

This equation in ${\displaystyle \varphi (t)}$ is solved via its characteristic polynomial

$${\displaystyle \lambda ^{2}+(a-1)\lambda +b=0.}$$

Now let ${\displaystyle \lambda _{1}}$ and ${\displaystyle \lambda _{2}}$ denote the two roots of this polynomial. We analyze the two main cases: distinct roots and double roots:

If the roots are distinct, the general solution is

$${\displaystyle \varphi (t)=c_{1}e^{\lambda _{1}t}+c_{2}e^{\lambda _{2}t},}$$

where the exponentials may be complex.

If the roots are equal, the general solution is

$${\displaystyle \varphi (t)=c_{1}e^{\lambda _{1}t}+c_{2}te^{\lambda _{1}t}.}$$

In both cases, the solution ${\displaystyle y(x)}$ may be found by setting ${\displaystyle t=\ln(x)}$ .

Hence, in the first case,

$${\displaystyle y(x)=c_{1}x^{\lambda _{1}}+c_{2}x^{\lambda _{2}},}$$

and in the second case,

$${\displaystyle y(x)=c_{1}x^{\lambda _{1}}+c_{2}\ln(x)x^{\lambda _{1}}.}$$

Example [edit]

Given

$${\displaystyle x^{2}u''-3xu'+3u=0\,,}$$

we substitute the simple solution x ^m :

$${\displaystyle x^{2}\left(m\left(m-1\right)x^{m-2}\right)-3x\left(mx^{m-1}\right)+3x^{m}=m\left(m-1\right)x^{m}-3mx^{m}+3x^{m}=\left(m^{2}-4m+3\right)x^{m}=0\,.}$$

For x ^m to be a solution, either x = 0, which gives the trivial solution, or the coefficient of x ^m is zero. Solving the quadratic equation, we get m = 1, 3. The general solution is therefore

${\displaystyle u=c_{1}x+c_{2}x^{3}\,.}$

Difference equation analogue [edit]

There is a difference equation analogue to the Cauchy–Euler equation. For a fixed m > 0, define the sequence f _m (n) as

$${\displaystyle f_{m}(n):=n(n+1)\cdots (n+m-1).}$$

Applying the difference operator to ${\displaystyle f_{m}}$ , we find that

$${\displaystyle {\begin{aligned}Df_{m}(n)&=f_{m}(n+1)-f_{m}(n)\\&=m(n+1)(n+2)\cdots (n+m-1)={\frac {m}{n}}f_{m}(n).\end{aligned}}}$$

If we do this k times, we find that

$${\displaystyle {\begin{aligned}f_{m}^{(k)}(n)&={\frac {m(m-1)\cdots (m-k+1)}{n(n+1)\cdots (n+k-1)}}f_{m}(n)\\&=m(m-1)\cdots (m-k+1){\frac {f_{m}(n)}{f_{k}(n)}},\end{aligned}}}$$

where the superscript ^(k) denotes applying the difference operator k times. Comparing this to the fact that the k-th derivative of x ^m equals

$${\displaystyle m(m-1)\cdots (m-k+1){\frac {x^{m}}{x^{k}}}}$$

suggests that we can solve the N-th order difference equation

$${\displaystyle f_{N}(n)y^{(N)}(n)+a_{N-1}f_{N-1}(n)y^{(N-1)}(n)+\cdots +a_{0}y(n)=0,}$$

in a similar manner to the differential equation case. Indeed, substituting the trial solution

$${\displaystyle y(n)=f_{m}(n)}$$

brings us to the same situation as the differential equation case,

$${\displaystyle m(m-1)\cdots (m-N+1)+a_{N-1}m(m-1)\cdots (m-N+2)+\dots +a_{1}m+a_{0}=0.}$$

One may now proceed as in the differential equation case, since the general solution of an N-th order linear difference equation is also the linear combination of N linearly independent solutions. Applying reduction of order in case of a multiple root m ₁ will yield expressions involving a discrete version ofln,

$${\displaystyle \varphi (n)=\sum _{k=1}^{n}{\frac {1}{k-m_{1}}}.}$$

(Compare with: ${\textstyle \ln(x-m_{1})=\int _{1+m_{1}}^{x}{\frac {dt}{t-m_{1}}}.}$ )

In cases where fractions become involved, one may use

$${\displaystyle f_{m}(n):={\frac {\Gamma (n+m)}{\Gamma (n)}}}$$

instead (or simply use it in all cases), which coincides with the definition before for integerm.

See also [edit]

• Hypergeometric differential equation
• Cauchy–Euler operator

References [edit]

1. ^ ^{a b c} Kreyszig, Erwin (May 10, 2006). Advanced Engineering Mathematics. Wiley. ISBN978-0-470-08484-7.
2. ^ Boyce, William E.; DiPrima, Richard C. Rosatone, Laurie (ed.). Elementary Differential Equations and Boundary Value Problems (10th ed.). pp. 272–273. ISBN978-0-470-45831-0.

Bibliography [edit]

• Weisstein, Eric W. "Cauchy–Euler equation". MathWorld.

Find a General Solution to the Cauchy-euler Equation

Source: https://en.wikipedia.org/wiki/Cauchy%E2%80%93Euler_equation

Share :